Goniometricke funkcie
Ako som uz spominal na konci rubriky o Pytagorovej vety, v tejto casti sa budem zaoberat goniometrickymi funkciami.
Definicia: Goniometricke funkcie vyjadruju vztah medzi velkostmi ostrych uhlov v pravouhlom trojuholniku a pomermi dlzok stran daneho trojuholniku... Mame trojuholnik ABC so stranami a,b,c:
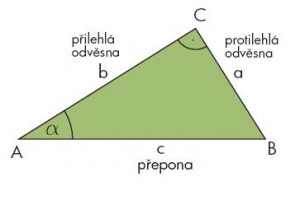
Plati potom vztahy
:
Toto pravidlo by platilo i keby sme chceli pocitat uhol naprotilahlom uhlu, teda uhlu pri bode B. V tomto pripade by sa strana a zmenila na přilehlu odvěsnu a strana b by sa zmenila na protilehlú odvěsnu. NO sposob pocitania by zostal rovnaky.
Obcas je lepsie a prehladnejsie goniometricke funkcie vyjadrovat pomocou tzv. jednotkovej kruznice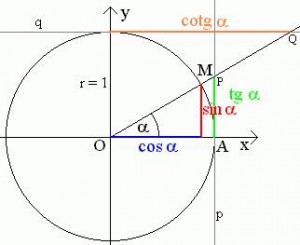
. Pomocou tejto kruznice su definovane funkcie sinus, cosinus, tangens a cotangens, kde mozme jasne vidiet vztahy odvesien a predpony.
Pre jednoduchost pocitania je mozne casto najst tabulku pre zakladne vypocty goniometrickych funkcii, ktore prevadzaju goniometricke funkcie zakladnych uhlov ako je 0°, 30° ,45° ,60° ,90° do zlomkoveho tvaru pre jednoduchsie pocitanie. Kedze sa mi dost casto stava, ze potrebujem pocitat uhly zlozitejsie nez su zakladne preto sem uvediem rozsirenu tabulku .
Ako mozeme vidiet, su tu prevody na zlomky aj pre neobvykle uhly ako je 18° ,36° , 67° 37` , atd. Samozrejme takych to prepoctov goniometrickych funkcii do zlomkoveho tvaru je nespocetne vela a odvodit si ich mozete i s trochou goniometrickych znalosti i sami. No vecsinou vam budu staciet tie zakladne
Goniometricke funkcie sa daju ece pocitat pomocou nekonecnyc radov a limit. V tomto pripade konkretne podla Taylorovho radu.
fakta o goniometrickych fciach:
- funkcia sin(x) je vzdy neparna fcia, plati sin(-x) = - sin(x)
- funkcia cos(x) je vzdy parna fcia, plati cos(-x) = cos(x)
- funkcia tg(x) je vzdy neparna fcia, plati tg(-x) = - tg(x)
- funkcia cotg(x) je vzdy neparna fcia, plati cotg(-x) = - cotg(x)
a nakoniec... casto vyuzivane vzorce, ktore sa vam budu urco hodit:
Zakladne kere potrebujete pre zakladne operacie s goniometrickymi funkciami
A taktiez vzorce kere budete potrebovat menej, ale obcas sa celkom hodia
Komentáře
Přehled komentářů
konecne rozumny komentar :)
Re: Re: no comment :D
(Hodinár, 26. 5. 2011 9:40)
To je ten problém že naše pani učiteľky ( učiťelia) matematiky učia bez toho že by žiakom ukázali praktické využitie matematiky ako takej v bežnom živote.
Napríklad nákup materiálu pri stavbe oprave domu, bytu, výrobe nábytku alebo rôznych strojársky súčiastkach. Nakoniec zistíš že ak niečo robíš používaš matiku celý život.
Re: Re: Re: no comment :D
(Cico Ciciak, 17. 11. 2016 12:43)Presne tak! Preto som nikdy nemal rád matiku!
Re: no comment :D
(Tibor, 24. 10. 2010 7:29)Všetko čo vieš sa Ti môže raz hodiť a preto nikdy nezačínaj s tým ,že načo mi to bude. Ja mám už nad 60 rokov a teraz chcem vymeniť krytinu na chatke. Má však pomerne malí spád a aby som vedel čo tam môžem dať, musím vedieť uhol strechy. Krytiny majú totiž udaný minimálny sklon strechy . (Keby som sa bol lepšie učil pred 40. rokmi, teraz by som nemal problém to vypočítať.
Re: Re: no comment :D
(santo 89, 27. 1. 2012 17:40)Presne tak, bez takýchto základných vecí sa človek v živote nepohne. Ale pokiaľ vám nevadí úmývanie verejných záchodov, vysýpanie smetiakov prípadne obživa prostredníctvom prostitúcie tak si tým hlavy zaťažovať nemusíte.
Re: zomieram
(lucifer, 22. 1. 2015 19:39)Butatot ak by si bol z toho madar tak by si tomu rozumel!!! Radsej umri!!!
Re: Re: zomieram
(smrt madarom, 29. 2. 2016 19:32)ty skurveny madar vyjebany aby ta jebla zimnica do rana ty bastard pokurveny
Re: zomieram
(Nukk, 18. 10. 2016 9:49)Hlavne ze madari sa znizili k tomu ucit sa po slovensky, pretoze madarsko upada stale ekonomicky dolu a aj mentalne. Z velkeho uhorska sa stala zumpa. Ja by som sa teda taky odporny ugrofinsky jazyk nechcel ucit
Domáca úloha
(Denisa, 21. 10. 2013 19:21)
Mohol by mi niekto poradit ako vypočítam príklad : tgx/1+tg(na druhu)x
Ďakuujem :))
priklad
(polki, 23. 4. 2013 21:37)a nemôžte mi vypočítať tento priklad ? :D sinx - sin(na tretiu)x / cosx - cos (na tretiu) x
Re: priklad
(Poctar, 23. 5. 2013 20:23)Zdravim, ten priklad sa rovna cotg x, riesenie je jednoduche, v citateli sin x roznasobis a zostane ti sin x(1 - cos(na druhu) x), potom to iste spravis aj v menovateli, len s cos x, no a (1- sin(na 2) x) je cos(na 2) x a (1 - cos(na 2) x) je sin(na 2) x, to potom uz iba prekratis a ostane ti cos x/ sin x a to je cotg x
domaca uloha
(Maria Tereza, 3. 4. 2013 15:44)ahoj mam na ulohu taký prikilad z matematiky a nerozumiem tomu : Odmerané hodnoty porovnajte s hodnotami uvedenými v tabulkach hodnot funkcie sinus ... a nemame k tomu nič ... iba tento text... Ďakujem
ja
(Kryo, 11. 5. 2012 12:46)v pripade ze by ste niecomu nechapali, kludne mi napiste na mail alebo na skype
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58
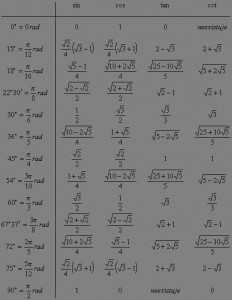
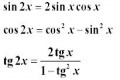
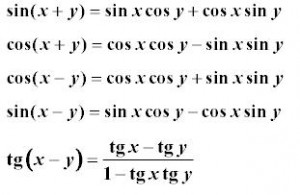
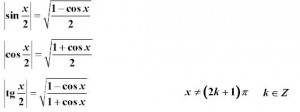
Re: Re: no comment :D
(ja som, 20. 1. 2011 20:13)