LIMITY A POSTUPNOSTI
Takze prejdeme k trochu tazsej matematike... k limitam Limity som nikdy nemal rad, preto mam o dovod viac sa tomu venovat
Limity som nikdy nemal rad, preto mam o dovod viac sa tomu venovat Kedze som nechapal teoriu, tu nacrtnem iba schemovite aby tomu aj taky lenivec ako ja pochopil na prvu supu a k tomu, nevytvaram matematicku encyklopediu, takze to nebudem ani nejako rozpisovat
Kedze som nechapal teoriu, tu nacrtnem iba schemovite aby tomu aj taky lenivec ako ja pochopil na prvu supu a k tomu, nevytvaram matematicku encyklopediu, takze to nebudem ani nejako rozpisovat no a priklady su iba o aplikovani vzorcov, takze to nebude az tak boliet.
no a priklady su iba o aplikovani vzorcov, takze to nebude az tak boliet.
Co su to teda limity?? Limita je matematicka konstrukcia, ktora vyjadruje ze sa hodnoty postupnosti alebo funkcie blizia k nejakemu cislu.
Limity pouzivame vtedy ak:
- Mame nespojitu funkciu a potrebujeme danu funkciu dodefinovat. Ako priklad by som uviedol delenie nulou. Kedze nulou delit nedokazeme, mozeme si ju dodefinovat ako cislo velmi bliziace sa k nule
- Ak mame postupnost konvergentnu
My sa budeme zaoberat hlavne limite postupnosti, kde plati, ze ak ma mat postupnost, musi byt konvergentna. Postupnost je konvergentna vtedy, ak pre kazde ε>0 existuje prirodzene cislo n0 , take ze pre vsetky n>n0 plati |xn - L| < ε, v opacnom pripade ide o postupnost divergentnu, teda napr. postupnost bliziaca sa k nekonecnu.
Kedze som nikdy nemal rad matematicke definicie a vzdy som bol radsej ked mi to niekto vysvetlil normalnou ludskou recou, takze sa o tom pokusim vlastnymi slovami
Takze konvergentna postupnost je kazda postupnost bliziaca sa k hocijakemu prirodzenemu cislu vratane nuly, teda moze to byt cisla 5, 500, 1, 0, 2342... atd. uvdme zopar prikladov:
Ako vidime, postupnost uvedena v priklade sa blizi k 1.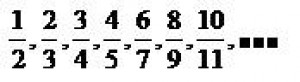 Kazda takato postupnost je mozna napisat v tvaru vzorcu
Kazda takato postupnost je mozna napisat v tvaru vzorcu![]()
Teraz ked sme uz zistili ze nasa postupnost je konvergentna, prv nez zacneme limitu pocitat musime zistit akeho typu mame limitu: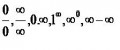 , az potom
, az potom mozeme vypocitat jej limitu v tomto pripade nastavime aby n sa blizila k nekonecnu. Takze nam vysiel pripad nekonecno/nekonecno. Musime teda pouzit "magicku nulku" (vid riesenie prikladu). Po tretej uprave vidime, ze vysledok vychadza 1, pretoze 1/n+1, kde n sa blizi k nekonecnu je 0. Samozrejme pripady 0/0 a nekonecno/nekonecno sa daju pocitat aj L'Hospitalovym pravidlom, ktory uvediem neskor.
mozeme vypocitat jej limitu v tomto pripade nastavime aby n sa blizila k nekonecnu. Takze nam vysiel pripad nekonecno/nekonecno. Musime teda pouzit "magicku nulku" (vid riesenie prikladu). Po tretej uprave vidime, ze vysledok vychadza 1, pretoze 1/n+1, kde n sa blizi k nekonecnu je 0. Samozrejme pripady 0/0 a nekonecno/nekonecno sa daju pocitat aj L'Hospitalovym pravidlom, ktory uvediem neskor.
Teraz by bolo vhodne uviest uzitocne vzorce pre postupnosti a limity, ktore by sa mohli v buducnu hodit. Zo zakladnych veci je treba snad zapametat, ze limita konstanty bude vzdy konstanta a limita cisla bliziace sa k neznamemu cislu bude dane cislo samotne. To a dalsie celkom lahke vzorce, ktore sa oplati 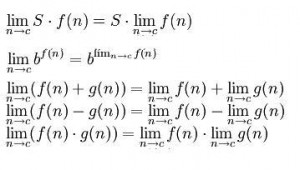 zapametat hodim na obrazok. Ostatne by to kcelo ece zapametat trochu teorie, ktore sa vam v buducnnu hodi, ale najdolezitejsie bude si zapametat vzorce uplne naspodku, pretoze hlavne tie budete pouzivat
zapametat hodim na obrazok. Ostatne by to kcelo ece zapametat trochu teorie, ktore sa vam v buducnnu hodi, ale najdolezitejsie bude si zapametat vzorce uplne naspodku, pretoze hlavne tie budete pouzivat
Komentáře
Přehled komentářů
MOC MĚ BAVÍ MATYKA A VÁS
:O prinosne, ale...
(Filip, 22. 5. 2013 15:17)
Nasiel som si tento clanok aby som sa z neho naucil limity na skusku z matiky ale nehnevaj sa, neda sa to citat... niGdy? neGdo?
Chapem ze nepises ucebnicu gramatiky a ze sa snazis ludom pomoct ale sorry, toto sa naozaj nedalo prehliadat...
Trochu si na tom daj zalezat a moze to byt velmi dobry zdroj informacii :)
re : Emilia
(Kryo, 13. 12. 2009 15:40)
hi, som rad ze ti stranka pomohla;) derivaty a integraly som mal v plane dokoncit, ale zabudol som heslo k mojmu acc:-((
take care
Ahoj
(Emilia, 15. 6. 2009 10:49)
Super stranka - gratulujem!
po dlhej pauze som sa rozhodla ist na vysku - na ekonomicku ( a to v zajranici). A tiez som totalne OUT z matiky. Este stastie ze som nasla tvoju stranku.
Chybaju mi tu derivaty a integraly.
Stiahla som si Calculus for dummies a Schaum's Outline Calculus - tiez je tam vsetko pekne rozpisane. -(len ak by si potreboval nejkay source)
TAk cau.
Take care...
re: priklad
(kryo, 4. 2. 2009 11:32)
To ano, ale nie kazdy pozna lhospitalovo pravidlo, ktory limitne priklady podstane zjednodusuje;)
Takze som ten priklad radsej rozpisal;)
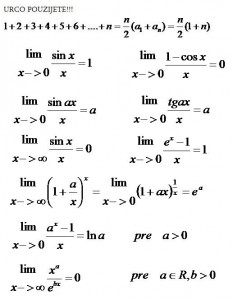

Natalie.Lamberska.
(natalie, 19. 9. 2013 18:10)