MATIKA

 TEORIA CISEL

Teoria cisel je vedna disciplina zaoberajuca sa vsetkym co sa cisel tyka. Ide o velmi rozsialu disciplinu, ktora sa potom deli na dalsi poddiscipliny podla toho o ake typy prikladov ide. Kedze nie je mozne vsetko obsiahnut v tejto stranke secko a tiez sa nekcem upisat k smrti Bude staciet, ak budete vediet, ze cisla vznikli uz v davnych dobach, pravdepodobne z potreby mat prehlad o roznych stavoch, povedzme aby sa praveky chovatel vedel ci mu nekdo nahodou necmajzol ovcu kym este chrapal

No prve zaznamy sa objavili az niekedy okolo 2000 rokov pnl. Od vtedy teoria cisiel ako disciplina presla dlhym a rychlym vyvojom az do dnesnej doby... no nebolo by dnes tam kde je bez roznych osobnosti ako:

• Euklidus - velky myslitel znamy pre Euklidovu vetu: "Obsah štvorca zostrojeného nad výškou pravouhlého trojuholníka spustenou na preponu sa rovná obsahu pravouholníka, ktorého strany sú úseky na prepone priľahlé k odvesnám." , v skratke v_c²=c_a.c_b
• Mersenne - znamy pre objav Mersenovo prvocislo, ktory ma tvar M_n=2ⁿ-1, kde n je prirodzene cislo. Postupnost prvych 5 Mersenovych prvocisel je 3, 7, 31, 127, 8191 ....
• Pierre de Fermat - znamy pre objav Velkej Fermatovej vety, ktora tvrdi: "Nejestvujú celé čísla x, y a z väčšie ako nula, pre ktoré by platilo xⁿ + yⁿ = zⁿ, kde n je prirodzené číslo väčšie ako 2."
• Leonard Euler - znamy pre Eulerovu vetu o mnohostenu, ktory tvrdi ze sucet poctu stien a vrcholov da vzdy cislo o 2 vecsie ako je pocet hran daneho mnohostenu.
• Andrew Wiles - dokazal "iba" vseobecnu platnost Velkej Fermatovej vety. Mozno nie az taka velka zasluha ale ak si otvorite stranku na wikipedii o nom, tak je tam moznost pozriet si jeho dokaz v formate pdf, ktory ma 10 Mb a pri nom varovanie kere ma celkom dostalo:"Upozornenie: Súbor má vyše 10 MB, je v angličtine a je úplne nezrozumiteľný pre každého, kto nemá doktorát z teórie čísel alebo blízko príbuzných odborov." Taq teras uz viem co bude mojim cielom na tejto stranke ... vysvetlit vam Wilesov dokaz ... hehe zartujem... keby som pochopil aspon prvu stranku jeho dokazu, tak by som vam o tom i nieco povedal, ale upozornenie neklamalo a ja mam od doktoratu z matiky velmi daleko

Je sice ece vela vyznamnych matematkov ale nechce sa mi ich prehladavat vsetkych, ak chcete o nich viac vediet, tak skuste wikipediu, odkaz na nu je v mojich oblubenych odkazov.

Vratme sa ale k zakladu teorii cisiel, teda ciselnym mnozinam:

• prirodzene cisla : cisla kere sa ako dieta ucime medzi prvymi, napr. 1, 2, 3, 4, .... , 19, 20, 21, 22, ....., 2342, .... , 4234353.... ma znacenie N. Ci je aj 0 prirodzene cislo sa polemizuje do dnes, presne to netusi nikdo, takze ani ja
• cele cisla : podobne ako prirodzene cisla, ale pridane o zaporne cisla a 0, napr.: ...-2424, ..., -3, -2, -1, 0, 1, 2, 3, .... 23435... ma oznacenie Z
• racionalne cisla: su vsetky cisla prevoditelne do zlomkov, napr.: 1/2, 3/4, 4/4,... ma oznacenie R
• iracionalne cisla: cisla nemozne previest do zlomkov, delime ich na algebraicke (napr. odmocnina z 3) a trancedentne(napr. ludolfovo cislo π), ma oznacenie I
• realne cisla: secky racionalne a iracionalne cisla dohromady, ma oznacenie R
• komplexne cisla: skladaju sa z realnej a imaginarnej casti, imaginarnu oznacujeme i , napriklad 1+i.
• prvocisla: opak zlozenych cisel, teda cisla ktore su delitenymi iba 1 a ono samym. Zaciatok rady prvocisel su 2, 3, 5, 7, 11, 13, 17, 19, .... Specialne pripady su Mersenove cisla, ktore som popisal uz hore. Pozn.: Ako vsetky mnoziny cisiel aj prvocisel je nekonecne vela.

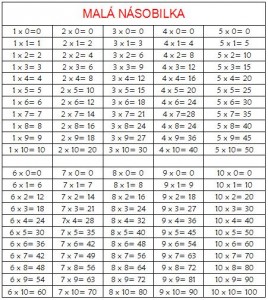
MALÁ NÁSOBILKA

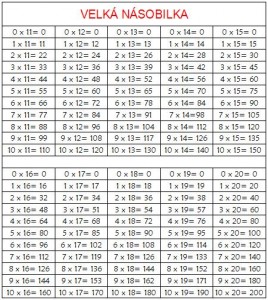
VELKÁ NÁSOBILKA

Predpokladám, že seci už násobilku ovladáte, takže som ju pridal iba pre komplexnosť:) ale kto vie, mozno budem chciet v 90tke vypocitat naky jednoduchy priklad a pamet uz nebude to co bolo, ono to tu zostane;) A v pripade, ze nasobilku neovladate, viete kde to najst;)