TIPY A HINTY
Snad najdolezitejsia cast, keru by mal kazdy dobry matik ovladat
V tejto rubrike si povieme jak sa ma pocitat zdravo, ziadne hrotenie... sice nikoho pocitanie este nezabilo, ale naco riskovat
takze tu uvediem zopar trikov jak si ulahcit zivot v matike hlavne v algebre, pri rieseni rovnic a zlomkov
Vecsina prikladov su chytaky na kere treba logicky, preto vzdy hladajte moznost jak dany zlomok vykratit alebo zjednodusit. Su aj caste pripady, profesori velmi casto take, 
ktore musite najrv rozsirit aby ste vobec dostali vysledok Take pripady sa vecsinou riesia pouzitim "specialnej jednicky" ako mozme vidiet na priklade1. V tomto pripade je princip jednoduchy, ide o rozsirenie zlomku nasobenim tak aby sa cely zlomok nasledne vysledok nezmenil... Preto sa rozsiruje o jednicku, pretoze x.1=x pre hociktore x.
Dalsi profesormi velmi oblubene priklady su na rozsirovanie 
pouzitim "magickej nulky". Tento priklad som uvidol aj v limitach, takze vam to sem znovu hodim. Princip je znovu jednoduchy. Princip spociva v scitani alebo odcitani cisla, ktore chceme pouzit pri uprave prikladu tak, aby sme priklad nezmenili a teda ani jeho vysledok. Takze dane cislo bud scitame alebo odcitame, no po pricitani ho musime i odcitat a naopak, po odcitani ho musime znovu pricitat aby sme priklad nezmenili
Magia je v tom, ze ho mozete pripocitat kolko kcete, a priklad abo vysledok sa nezmeni. Supa ne?!?
A zivot je hned o nieco snadnejsi...
Teraz sa ale uz vratme ku krateniu a zjednodusovaniu. Najcastejsie pojde o kratenie podla vzorcekov:
-
a2 - b2 = (a - b)(a + b)
-
(a + b)2 = (a + b)(a + b) = a2 + 2ab + b2
-
(a - b)2 = (a - b)(a - b) = a2 - 2ab + b2
-
(a + b)3 = a3 + 3a2b + 3ab2 + b3
-
(a - b)3 = a3 - 3a2b + 3ab2 - b3
Dalsia uzitocna pomocka je vediet rozkladat zlomky, hodi sa hlavne pri intergraloch a derivaciach. Princip spociva v tom, ze priklad s velmi slozitym menovatelom nedokazeme vyriesit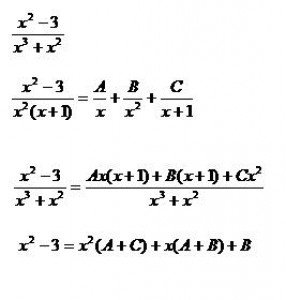 
klasickym sposobom, alebo by bolo velmi narocne na cas. Preto sa menovatel rozlozi na niekolko mensich. Rozklada sa dovtedy kym nezahrnemie vsetky mocniny a cleny menovatela, takze neznamych nemusi byt iba 3 (A, B, C) ako mam v priklade ale moze ich byt aj 10, ale vecsinou sa v beznych prikladoch vyskytuju tak do 5 neznamych. Po uprave v poslednom kroku vidime ze
A + C = 1
A +B = 0
B = -3 ⇒ A =3 ⇒ C = -2 ⇒ takze vysledok rozkladu bude
Snad vam tieto triky a hinty pomozu vo vasom pocitani ci uz v skole abo v starobe, kazdopadne na vsetko treba logicky a troxu tricky aby ste neskoncili jak tento:
Komentáře
Přehled komentářů
neznasam matyku
Re: komentar
(Pepega, 5. 12. 2020 14:32)Ako tak čítam tvoj komentár, tak ty naznášaš aj slovenský jazyk
Recommendations: how to promote your matika.estranky.cz
(Latonyacob, 26. 3. 2018 0:01)
Tato zpráva je zde zveřejněna pomocí programu XRumer + XEvil 4.0
XEvil 4.0 je revoluční aplikace, která může obejít téměř veškerou ochranu proti botnetu.
Captcha Rozpoznávání Google (ReCaptcha-1, ReCaptcha-2), Facebook, Yandex, VKontakte, Captcha Com a více než 8,4 milionu dalších typů!
Četl jste to - to znamená, že to funguje! ;)
Podrobnosti na oficiálních stránkách XEvil.Net, je bezplatná demo verze.
re: drobnost
(kryo, 25. 3. 2009 4:07)
Menovatel rozkladas vzdy tak jak to zadanie vyzaduje;
povedzme ze v zadani by bol
x^3(x+1) tak ho rozlozis na x a x^2 a x^3 a (x+1)
povedzme ak by tam bol x^3(x+1)(x-2), tak ho rozdelis na x a x^2 a x^3 a (x+1) a (x-2)
Je to relativne jednoduche, kce to iba cvika.
jedna drobnost
(filo.soph, 12. 2. 2009 16:15)Dobry clanocek. Akurat mi nedochadza jedna drobnost z posledneho prikladu. Ako sa rozlozi zlomok, ktory ma zlozeny vyraz v menovateli. Vie mi niekto vysvetlit, co sa robi s menovatelom v tom druhom kroku, pri dosadeni neznamych A,B,C?
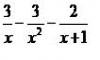
komentar
(lich, 19. 4. 2009 16:00)