Pytagorova veta
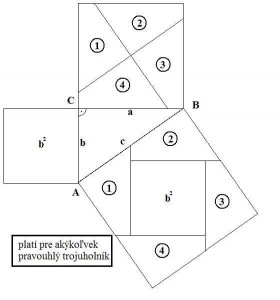
Pre pytagrovu vetu plati, ze obsah štvorca zostrojeného nad preponou (najdlhšou stranou) pravouhlého trojuholníka je rovný súčtu obsahov štvorcov zostrojených nad jeho odvesnami.
a2 + b2 = c2
V pripade, ze by ste si chceli overit ze je to skutocne plati, som rozdelil stvorce nad priponou do nikolko casti a poskladal u predpony aby to pekne sedelo.
Samozrejme, tento sposob neplati iba pre stvorce ale pre hociktory utvar... pre inspiraciu vam sem hodim este niekolko moznosti.
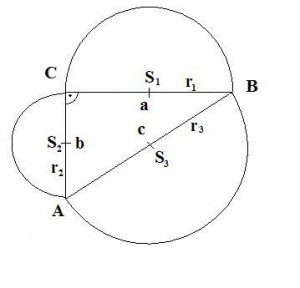
Napriklad v tomto pripade su sucty obsahov polkruhu nad priponou sa rovna obsahu polkruhu nad predponou. Alebo mozme povedat, ze vseobecne plati, ze sucet obsahov utvarov zostrojeneho nad priponami sa rovna obsahu utvaru zostrojeneho nad predponou A pre lenivejsich ako ja, ak by ste vobec nechceli pocitat vzorce na druhu, tak tu mate jednoduchy bezmocninovy vzorec na vypocet: Nesmieme ale zabudnut i na nepravouhle trojuholniky, pretoze i na nich je mozne vyuzit pytagorovu vetu. Takato veta sa nazyva uplna pytagorova veta a plati: c2 = a2 + b2 - 2.a.b.cosα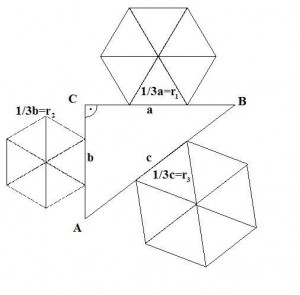
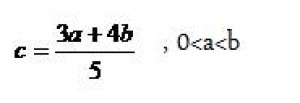
Teraz asi nastava otazka co je ten cosα
goniometricke funkcie vysvetlim v nasledujucej rubrike
čuus
(Argy, 10. 10. 2008 9:04)