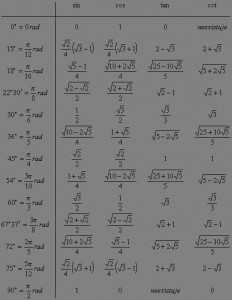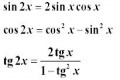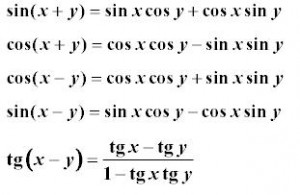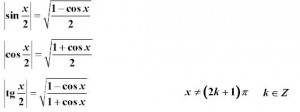Goniometricke funkcie
Ako som uz spominal na konci rubriky o Pytagorovej vety, v tejto casti sa budem zaoberat goniometrickymi funkciami.
Definicia: Goniometricke funkcie vyjadruju vztah medzi velkostmi ostrych uhlov v pravouhlom trojuholniku a pomermi dlzok stran daneho trojuholniku... Mame trojuholnik ABC so stranami a,b,c:
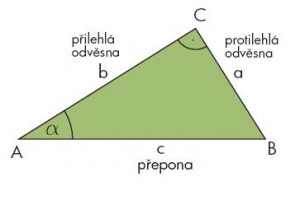
Plati potom vztahy
:
Toto pravidlo by platilo i keby sme chceli pocitat uhol naprotilahlom uhlu, teda uhlu pri bode B. V tomto pripade by sa strana a zmenila na přilehlu odvěsnu a strana b by sa zmenila na protilehlú odvěsnu. NO sposob pocitania by zostal rovnaky.
Obcas je lepsie a prehladnejsie goniometricke funkcie vyjadrovat pomocou tzv. jednotkovej kruznice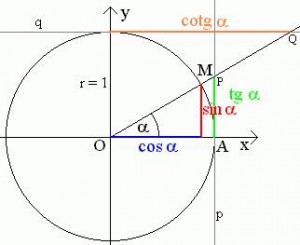
. Pomocou tejto kruznice su definovane funkcie sinus, cosinus, tangens a cotangens, kde mozme jasne vidiet vztahy odvesien a predpony.
Pre jednoduchost pocitania je mozne casto najst tabulku pre zakladne vypocty goniometrickych funkcii, ktore prevadzaju goniometricke funkcie zakladnych uhlov ako je 0°, 30° ,45° ,60° ,90° do zlomkoveho tvaru pre jednoduchsie pocitanie. Kedze sa mi dost casto stava, ze potrebujem pocitat uhly zlozitejsie nez su zakladne preto sem uvediem rozsirenu tabulku .
Ako mozeme vidiet, su tu prevody na zlomky aj pre neobvykle uhly ako je 18° ,36° , 67° 37` , atd. Samozrejme takych to prepoctov goniometrickych funkcii do zlomkoveho tvaru je nespocetne vela a odvodit si ich mozete i s trochou goniometrickych znalosti i sami. No vecsinou vam budu staciet tie zakladne
Goniometricke funkcie sa daju ece pocitat pomocou nekonecnyc radov a limit. V tomto pripade konkretne podla Taylorovho radu.
fakta o goniometrickych fciach:
- funkcia sin(x) je vzdy neparna fcia, plati sin(-x) = - sin(x)
- funkcia cos(x) je vzdy parna fcia, plati cos(-x) = cos(x)
- funkcia tg(x) je vzdy neparna fcia, plati tg(-x) = - tg(x)
- funkcia cotg(x) je vzdy neparna fcia, plati cotg(-x) = - cotg(x)
a nakoniec... casto vyuzivane vzorce, ktore sa vam budu urco hodit:
Zakladne kere potrebujete pre zakladne operacie s goniometrickymi funkciami
A taktiez vzorce kere budete potrebovat menej, ale obcas sa celkom hodia
